Quantifying Improvements to Streamflow Forecasts Stemming from Improved Soil Moisture Observations
Randal Koster June 2013
Operational forecasts of streamflow have historically been made using statistical models built on regressions computed across available observations (Garen 1992). An alternative approach to making forecasts involves the use of distributed land surface models that represent the physical processes relating precipitation to streamflow production (Wood and Lettenmaier 2006). While promising, use of such models is limited in part by the availability of the distributed datasets needed to initialize and otherwise constrain them. If improved versions of these data were to become available, streamflow forecasts using the distributed modeling approach should become more accurate.
One critically needed quantity is soil moisture. The recent launch of the Soil Moisture and Ocean Salinity (SMOS) satellite and the upcoming launch of NASA's Soil Moisture Active Passive (SMAP) satellite will provide scientists with high resolution soil moisture information that should, in principle, lead to improved initializations for land surface models producing streamflow forecasts. The GMAO has been heavily involved in the SMAP project and will be responsible for producing high resolution root-zone soil moisture products (and improved surface products, through data assimilation) from the raw data provided by the SMAP observing platform. In anticipation of SMAP's 2014 launch, the GMAO has performed a series of modeling experiments aimed at quantifying how improvements in soil moisture information might translate into improved streamflow forecasts.
The study utilized the Catchment land surface model (LSM), the same LSM used in MERRA. This LSM considers a full range of physical processes to determine the fluxes constituting the surface energy and water budgets, but unlike many other LSMs, GMAO's Catchment LSM explicitly accounts for subgrid variability in moisture regimes, as determined by topography and water availability (Koster et al 2000). The present study consisted of a number of sets of offline streamflow forecasts, each set performed under different assumptions. The first set, consisting of the "control" forecasts, utilized the best possible estimates of soil moisture initial conditions, as determined from analysis of antecedent meteorological conditions. In essence, these initial conditions were generated by integrating the LSM with observations-based forcing for multiple decades. Each control forecast ran at 0.5° resolution for three months; the different forecasts started on January 1, April 1, July 1, or October 1 for each year from 1920 to 2002. Climatological forcing and snow initial conditions were applied during the forecast period, so that all skill would be derived from the soil moisture initialization. The skill of these forecasts was quantified relative to observed streamflows, using the correlation between them as the skill metric.
In the next set of forecasts, a well-quantified, artificial level of error was added to the soil moisture initial conditions, and the forecasts proceeded as before. Because the error imposed was random (though spatially correlated with a prescribed correlation length scale), the forecast suite was repeated a number of times to provide an ensemble of forecasts with the given prescribed error level. Forecast skill relative to the observations was quantified for this set of forecasts. Due to the error imposed, the skill was reduced from that of the control set.
Subsequent collections of forecasts proceeded in the same way, but with different levels of error applied. In all, six levels of error were utilized, allowing us to determine a relationship between imposed level of error and the degradation of forecast skill.
Some basic results are shown in Figure 1. Each row in the figure corresponds to a basin for which we had access to naturalized streamflow measurements for the determination of skill. The four columns correspond to the four seasons examined (JFM corresponds to January through March, AMJ corresponds to April though June, and so on.) Within each panel, the x-axis represents the degree to which the initial soil moistures used agree with those of the control set of forecasts (in terms of the correlation coefficient), so that a larger imposed error corresponds to a lower value on that axis. Accordingly, an x-axis value close to one would imply a very low level of imposed error. The y-axis is the level of streamflow forecast skill achieved.
Clearly seen in the plots, for every basin and in every season, is a reduction in forecast skill with an increase in imposed soil moisture error. Indeed, the relationship between the forecast skill and the soil moisture error metrics is essentially linear for all cases and, for most of them, is a direct linear relationship. For larger basins, such as those toward the top of Figure 1, the skill of the forecasts is less sensitive to the error imposed on the soil moisture fields, a reflection of the fact that the error decorrelation length scale used in the experiments is significantly smaller than the size of these basins. In some of the smaller basins, forecast skill appears to fall off relatively quickly with imposed error, a reflection of certain nonlinearities that manifest themselves in the system.
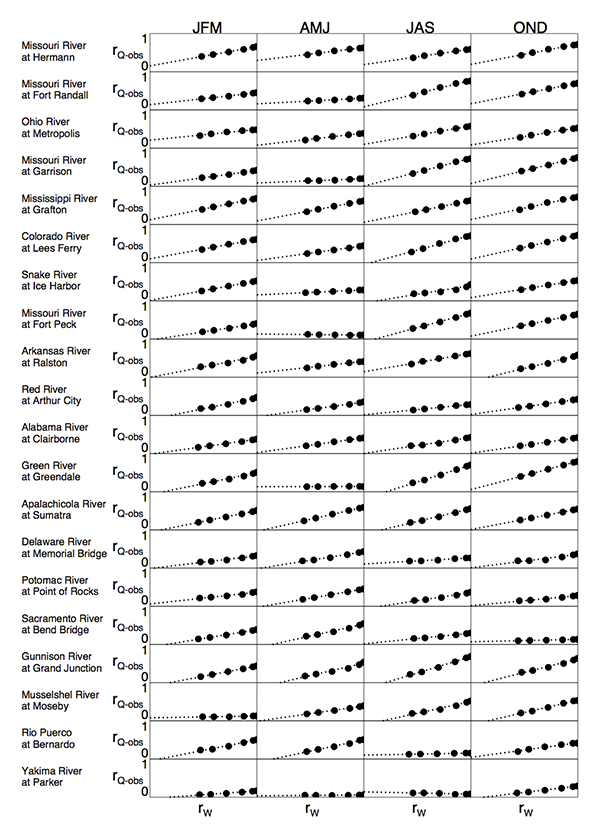
Click for larger image
We do not, of course, know how accurate the soil moisture initialization in the control forecasts is in the first place. There is certainly some error in these initializations, and the error could be large. The expectation is that data from the SMOS and SMAP satellite missions will lead to reductions in the errors of these current "best estimates".
Given this expectation, the linearity seen in Figure 1 has important implications for the impact of the error reduction on streamflow forecast skill. In essence, we can utilize the linearity, and the fact that the errors imposed here are, by construction, independent of the true errors, to estimate the derivative describing the increase in streamflow forecast skill associated with a given improvement in the soil moisture initialization. What we actually quantify, given that we don't know the true soil moistures, is the minimum value of this derivative; actual improvement would be higher than that suggested by this minimum. Details of this interpretation of the figure and quantitative estimates for the minimum values of derivatives are provided by Koster et al. (2013).
Our simulations suggest that hydrological forecasts of streamflow, and associated water resource management practices, do stand to benefit from the high quality soil moisture information that space-based sensors like SMAP will provide.
References
Garen, D. C., 1992: Improved techniques in regression-based streamflow volume forecasting. J. Water Resource Planning and Management, 118, 654-670. doi: 10.1061/(ASCE)0733-9496(1992)118:6(654)
Koster, R. D., G. K. Walker, S. P. P. Mahanama, R.H. Reichle, 2013: Soil moisture initialization error and subgrid variability of precipitation in seasonal streamflow forecasting. Manuscript submitted to J. Hydrometeorology.
Koster, R. D., M. J. Suarez, A. Ducharne, M. Stieglitz, and P. Kumar, 2000: A catchment-based approach to modeling land surface processes in a GCM, Part 1, Model Structure. J. Geophys. Res., 105, 24809-24822. doi: 10.1029/2000JD900327
Wood, A. W., and D. P. Lettenmaier, 2006: A test bed for new seasonal hydrologic forecasting approaches in the Western United States. Bull. Am. Met. Soc., 87, 1699-1712. doi: 10.1175/BAMS-87-12-1699

